Chambolle-Pock Algorithm for Solving LASSO

This note aims at showing how to solve LASSO by using Chambolle-Pock (CP) algorithm at the most basic level. CP is a primal-dual method solving both the primal and dual problem at the same time. However, it is important to notice that the iterative dual solutions are not guaranteed to be feasible.

The code for this post is available on my Github.

Basic of Chambolle-Pock Algorithm

Problem:

Primal and dual problem

$$\min_{x} \quad f(Ax) + g(x)$$

$$\max_{u} \quad -f^*(u) - g^*(-A^Tu)$$

Initialization: $\tau, \sigma>0, \theta\in [0,1]$, $\overline x_0 = x_0\in X$ and $u_0 \in V$. Here one should choose $\tau=\sigma < 1/||A||$.

Iteration:

$$\begin{aligned} u^{(k+1)} & = \text{prox}_{\sigma f^*}(u^{(k)} + \sigma A\overline x^{(k)})\\ x^{(k+1)} & = \text{prox}_{\tau g}(x^{(k)} - \tau A^T u^{(k+1)})\\ \overline x^{(k+1)} & = x^{(k+1)} +\theta (x^{(k+1)} - x^{(k)}) \end{aligned}$$

Applying on LASSO

The LASSO setup has primal and dual problem defined as follows

$$\min_{x} \quad \frac{1}{2}||b-Ax||^2_2+ \lambda ||x||_1$$

$$\max_{u} \quad \frac{1}{2}||b||^2_2 - \frac{1}{2}||b-u||^2_2 - I(||A^Tu||_\infty\leq \lambda)$$

Here, the dual optimal solution $u^\star$ is the closest point projection of $b$ onto $U = \{u: ||A^Tu||_\infty\leq \lambda\}$.

This dual problem is a little bit different from aforementioned dual problem since we set $$u:= -u,$$ this is possible since $U$ is symmetric, i.e. $-U=U$.

We obtain such above dual problem since

$$f(v) = \frac{1}{2}||b-v||^2_2, \quad f^*(u) = \frac{1}{2}||b+u||^2_2 - \frac{1}{2}||b||^2_2$$

and

$$g(x) = \lambda ||x||_1, \quad g^*(z) = \lambda I(||z/\lambda||_\infty\leq 1)$$

Let $u^+ = prox_{\sigma f^*} (u)$, then we should have

$$\sigma(u^++b) + (u^+-u) =0 \Longleftrightarrow u^+ = \frac{u - \sigma b}{1+\sigma}$$

and let $x^+ = prox_{\tau g} (x)$, this is soft thresholding operator evaluated by

$$x^+ = sign(x) [|x| - \tau \lambda]_+$$

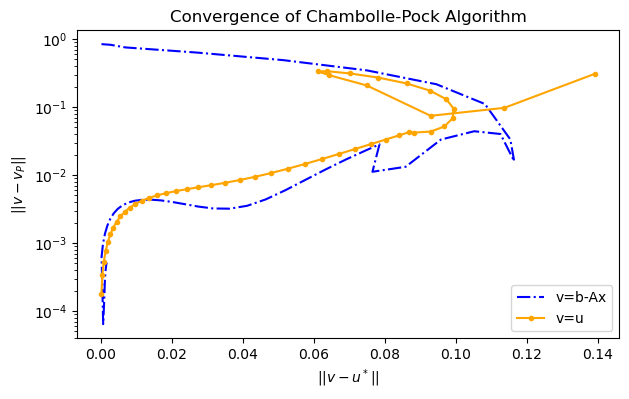
The following figues illustrates the convergence of CP for a LASSO problem with dual problem in $\mathbb R^2$

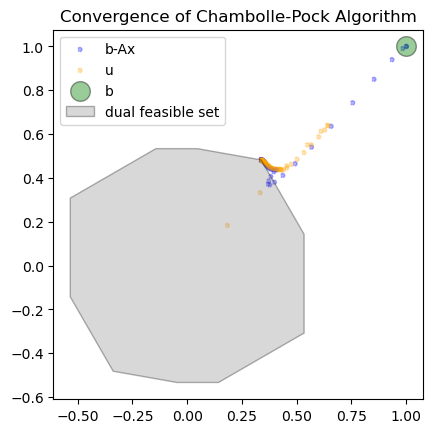
Remark. Here since the dual solutions $u$ obtained from the CP are not dual feasible, we can not use the dual gap as a stopping metric/condition as usual. Here we consider another quite interesting metric as follows. Let $P$ be the hyper-plane defined by $\{u: \langle Ax^\star, u\rangle = \lambda ||x^\star||_1\}$. Then it is clear by the optimality condition that $u^\star\in P$, So for a point $v$ converging to $u^\star$, we can quantify the convergence of $v$ by two quantities $(||v_P-u^\star||, ||v -v_P||)$, where $v_P$ is the projection of $v$ onto $P$, which can be computed in closed form. Here $v=b-Ax$ or $v=u$ for $x\rightarrow x^\star$ and $u\rightarrow u^\star$.

Code

The full code is available on my Github. Here we provide the main CP procedure written in Python.

def dual_prox(b, p, sigma):
	return (p - sigma*b )/ (1+sigma)

def primal_prox(z, lbd, tau):
	return np.sign(z) * np.maximum(np.abs(z) - lbd*tau, 0.)

def lasso_chambolle_pock(A, b, lbd, max_iters=100):
	x0 = np.zeros(A.shape[1])
	u0 = np.zeros(A.shape[0])
	lip = np.sqrt((A**2).sum())
	sigma = 0.5/lip
	tau = 0.5/lip
	theta=1

	x = x0.copy()
	u = u0.copy()
	xbar = x0.copy()
	x_list = []
	u_list = []

	for i in range(max_iters):
		xpre = x.copy()
		u = dual_prox(b, p= u + sigma * A @ xbar, sigma=sigma)
		x = primal_prox(z= xpre - tau * A.T @ u, lbd=lbd, tau=tau)
		xbar = x + theta * (x-xpre)

		x_list += [x]
		u_list += [u]

	x_array= np.vstack(x_list).T
	u_array = np.vstack(u_list).T # change sign of u
	return x_array, u_array



x_array, u_array = lasso_chambolle_pock(A, b, lbd, max_iters=50)
u_array = -u_array # remember to change sign of u suitable for our dual problem
r_array = b.reshape(2, 1) - A @ x_array