KL Projection using Cvxpy Python

Kullback_Leibler Projection using Python package Cvxpy

This post shows you how to solve a convex optimization problem using Cvxpy - a Python package. Here, the problem instance we consider is the projection from a point onto a simplex using Kullback-Leibler divergence.

Specifically, we consider the following optimization problem:

$$\begin{align*}\min_{x\in \mathbb R^n} \quad & KL(x, c)\\ s.t. \quad & \sum_{i=1}^n x_i=1,\\ & x\geq 0.\end{align*}$$

Here $KL(x, c)$ is the Kullback-Leibler divergence between positive vectors $x$ and $c$. It is non-negative and convex in $x$ with definition given by:
$$KL(x, c) = \sum_{i=1}^n x_i \log(x_i/c_i)-x_i +c_i$$

The Python code for solving this problem is provided below:

import cvxpy as cp
import matplotlib.pyplot as plt 
import numpy as np
np.random.seed(123)

n = 30
x = cp.Variable(n)
ones  = np.ones(n)
c = np.random.rand(n)
c = c/c.sum()
c = c * 1.2

objective = cp.Minimize(ones.T @ cp.kl_div(x, c))
constraints = [ones.T @ x == 1, 0<=x]
problem = cp.Problem(objective, constraints)
problem.solve()

# print("Optimal value:", problem.value)
# print("Optimal solution:", x.value)

plt.plot(x.value, color="blue", label="estimated")
plt.plot(c, color="red", label="true")
plt.legend()
plt.ylim(0.)
plt.show()

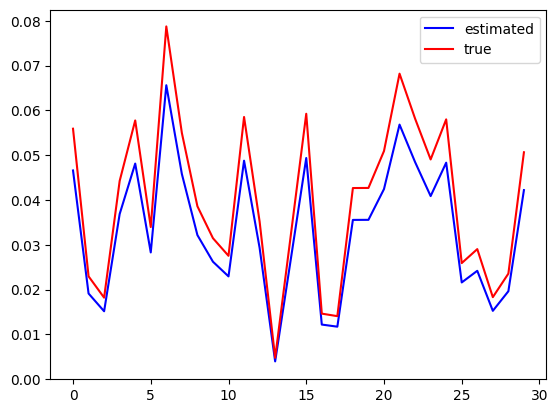
The obtained result is given in the following figure.