category-group-groupoid

Exploring Algebraic Structures: Categories, Groups, and Groupoids

In modern mathematics, algebraic structures offer a powerful language for expressing symmetry, computation, and relationships between objects. In this post, we’ll explore three fundamental structures: categories, groups & monoids, and groupoids. Each section introduces the basic definitions and gives concrete examples to bring the abstract concepts to life.

1. Categories and the Category of Sets

A category is a mathematical structure that abstracts the idea of objects and the relationships (called morphisms) between them. Categories provide a unified framework for discussing many different mathematical systems.

Definition: Category

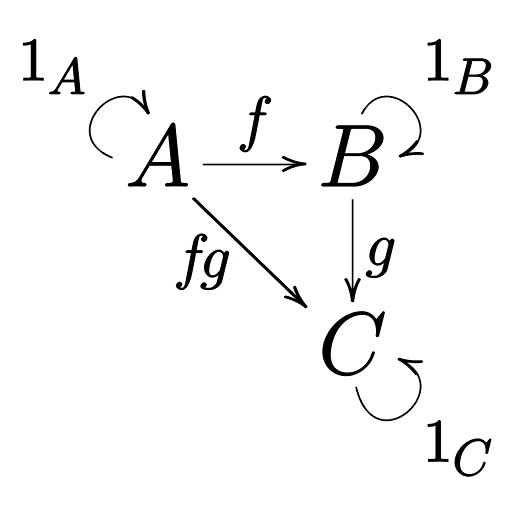
A category $\mathcal{C}$ consists of:

A collection of objects (denoted $A, B, C, \dots$ ),
A collection of morphisms (also called arrows) between objects. A morphism $f: A \to B$ goes from object $A$ to object $B$ ,
For each object $A$ , an identity morphism $\mathrm{id}_A: A \to A$ ,
A composition rule: if $f: A \to B$ and $g: B \to C$ , then there is a morphism $g \circ f: A \to C$ .

They must satisfy:

Associativity:

$h \circ (g \circ f) = (h \circ g) \circ f$ ,
Identity laws:

$\mathrm{id}_B \circ f = f = f \circ \mathrm{id}_A$

Example: The Category of Sets

The most familiar category is $\mathbf{Set}$ , where:

Objects are sets (like $\mathbb{N}, {a, b}, \emptyset$ ),
Morphisms are functions between sets,
Composition is the usual function composition,
Identity morphism is the identity function $\mathrm{id}_A(x) = x$ .

In $\mathbf{Set}$ , associativity and identity laws are satisfied naturally by function composition.

2. Groups and Monoids

Groups and monoids are algebraic structures that capture the idea of combining elements.

Definition: Monoid

A monoid is a set $M$ with:

A binary operation $\cdot: M \times M \to M$ (often written as multiplication),
An identity element $e \in M$ ,

such that:

Associativity: $(a \cdot b) \cdot c = a \cdot (b \cdot c)$ for all $a, b, c \in M$ ,
Identity: $e \cdot a = a = a \cdot e$ for all $a \in M$ .

Definition: Group

A group is a monoid where every element also has an inverse. That is:

For each $a \in G$ , there exists $a^{-1} \in G$ such that

$a \cdot a^{-1} = e = a^{-1} \cdot a$

Example: Integers and Natural Numbers

The set $\mathbb{Z}$ of integers with addition forms a group:
- Identity: $0$ , inverse of $a$ is $-a$ .
The set $\mathbb{N}$ (non-negative integers) with addition forms a monoid:
- Identity: $0$ , but most elements don’t have inverses (no negative numbers), so it’s not a group.

Groups capture symmetry—you can do and undo an operation. Monoids capture processes—you can combine actions, but not necessarily undo them.

3. Groupoids and Symmetries with Partial Inverses

A groupoid generalizes the idea of a group by allowing partial symmetries between different objects. Instead of a single set, we now think in terms of objects and invertible morphisms.

Definition: Groupoid

A groupoid is a category where:

Every morphism is invertible, i.e., for every $f: A \to B$ , there exists $f^{-1}: B \to A$ such that

$f \circ f^{-1} = \mathrm{id}_B \quad \text{and} \quad f^{-1} \circ f = \mathrm{id}_A$

In other words, a groupoid is like a group, but with possibly many objects, and morphisms only between some pairs of objects.

Example: The Fundamental Groupoid of a Space

Let $X$ be a topological space. The fundamental groupoid $\Pi_1(X)$ is a groupoid that captures how points in $X$ are connected by paths (up to deformation). It is defined as follows:

Objects: the points of $X$ .
Morphisms: a morphism from $x \in X$ to $y \in X$ is a homotopy class of paths from $x$ to $y$ .

A path from $x$ to $y$ is a continuous function:

$\gamma: [0, 1] \to X \quad \text{with} \quad \gamma(0) = x, \quad \gamma(1) = y$

Two paths $\gamma_0$ and $\gamma_1$ from $x$ to $y$ are considered equivalent if there exists a homotopy between them—i.e., a continuous function:

$H:[0,1]×[0,1]→X$

such that:

$H(t,0)=γ_0(t),H(t,1)=γ_1(t)$

for all $t, s \in [0,1]$ . This ensures the endpoints stay fixed during the deformation.
Composition: if $[\gamma_1]: x \to y$ and $[\gamma_2]: y \to z$ are morphisms, then their composition is the homotopy class of the concatenated path:

$[γ_2*γ_1]:x→z$

where $(\gamma_2 * \gamma_1)(t)$ first follows $\gamma_1$ from $x$ to $y$ , then $\gamma_2$ from $y$ to $z$ (reparametrized to fit in $[0,1]$ ).
Inverses: each path $\gamma: x \to y$ has an inverse path $\gamma^{-1}: y \to x$ given by:

$\gamma^{-1}(t) = \gamma(1 - t).$

This defines an inverse morphism $[\gamma^{-1}]: y \to x$ .

Connection to the Fundamental Group

If we fix a base point $x \in X$ , then the set of morphisms from $x$ to itself in the groupoid $\Pi_1(X)$ forms a group, called the fundamental group of $X$ at $x$ , denoted $\pi_1(X, x)$ .

So $\pi_1(X, x)$ is a group of loops at $x$ up to homotopy, with group operation given by concatenation of loops.

This shows that the fundamental group is just a special case of the more general structure of a groupoid, where we allow paths between all points in $X$ , not just loops based at a single point.

Closing Thoughts

These algebraic structures—categories, monoids, groups, and groupoids—form the language of modern mathematics, from algebra and geometry to computer science and logic. Understanding them provides a unifying perspective and opens doors to deeper theory, including functors, natural transformations, and higher category theory.