Solving L1-Penalization of Kullback-Leibler Divergence using SMART Algorithm

Author: Tran Thu Le
Date: 7/3/2023
Abstract: In this note, we show how to modify the SMART-algorithm to solve the Sparse regression of Kullback-Leibler divergence using L1-pennalization.

Preliminaries

For vectors $x, y$ in a finite dimensional vector space, we denote by $xy$, $x/y$, $\log x$ if $x\geq 0$ and $\exp x$ the vectors with operators applied elementwise. Here we set $\log 0=-\infty$.

For $u, v\in \mathbb R^m$, the negative entropy is a convex function defined by

$$H(u) = \langle u, \log u\rangle = \sum_{u_i>0} u_i \log(u_i).$$

where $u\geq 0$. Notice that $H(0)=0$.

The Bregman divergence of a convex function $h$ is

$$Breg_h(v, p) = h(v) - h(p) - \langle \nabla h(p), v-p\rangle.$$

The Kullback-Leibler divergence (a.k.a. relative entropy) is the Bregman divergence of negative entropy

$$KL(v, p) = Breg_H(v, p) = \langle v, \log \frac{v}{p}\rangle - \langle 1, v\rangle + \langle 1, p\rangle.$$

where $v$ and $p$ have the same signs, i.e. $v/p\geq 0$ and $p_i\neq 0$ for all $i=1,..., m$.

One should have 2 remarks. First, KL div. has gradient of the form

$$\nabla_v KL(v, p) = \nabla H(v) - \nabla H(p) = \log \frac{v}{p}.$$

This holds for any same sign vectors $v, p$.

Second, the Bregman div. satisfies the following Cosine law

$$Breg_h(v', b) = Breg_h(v', v) + Breg(v, b) - \langle v'-v, \nabla h(b) - \nabla h(v)\rangle.$$

If we let $f(v):=Breg_h(v, b)$ for some given $b\in \mathbb R^m_+$, we have

$$Breg_f(v', v) = f(v') -f(v) - \langle \nabla f(v), v'-v\rangle=Breg_h(v', v)$$

We call this the Bidual Bregman div. theorem.

Sparse-SMART algorithm

Simultaneous Multiplicative Algebraic Reconstruction Technique (SMART) is an iterative method to solve Kullback-Leibler divergence (KL div.) problem, see [1]. We now show how to use a modification of SMART, say Sparse-SMART, to solve the following sparse convex problem

$$P(x) = KL(Ax, b) +I(Ax\geq 0) + \lambda ||x||_1 + I(x\geq 0).$$

where $A=[a_1,...,a_n]\in \mathbb R^{m\times n}$ with $a_i\geq 0$, $b\geq 0$, $\lambda >0$. Note that $x\geq 0 \Rightarrow Ax\geq 0$, without the condition $x\geq 0$, the constraint $Ax\geq 0$ should be explicitly declared.

This problem aims to solve the linear inverse problem $Ax=b$ using KL div as a distance between $Ax$ and $b$ and the optimal solution tends to be sparse due to the use of L1-norm. Note that by the non-negativity constraint $x\geq 0$, we have $||x||_1=\langle 1, x\rangle$. Here, w.l.o.g we assume that

$$||a_i||_1 =1, \forall i=1,..., n.$$

Under this assumption we have, see [Prop. 2, [1]]

$$KL(Ax', Ax)\leq KL(x', x).$$

Let $f(v) = KL(v, b)$ we have

$$Breg_f(Ax', Ax) = Breg_H(Ax', Ax) = KL(Ax', Ax) \leq KL(x', x)$$

So for $x', x \geq 0$, we have

$$P(x') \leq f(Ax) + \langle A^T \nabla f(Ax), x'-x\rangle + \lambda \langle 1, x'\rangle + KL(x', x)= \varphi_x(x')$$

Then $\varphi_x$ achieves its min value at $x'$ being the solution of the following equation

$$A^T \nabla f(Ax) + \lambda + \log \frac{x'}{x}=0$$

Then

$$x' = x \exp(-A^T\nabla f(Ax) - \lambda)$$

Let $r_x=-\nabla f(Ax)$ the residual of $x$, the formula of $x'$ can be rewritten

$$x' = x \exp(A^Tr_x - \lambda).$$

Explicitly, the Sparse-SMART update rule for our problem is as follows

$$x^{(k+1)} = x^{(k)} \exp(A^T\log \frac{b}{Ax^{(k)}} - \lambda)\tag{Sparse-SMART}$$

Note. 1) If $\lambda >\lambda_{\max}:= \max A^T b$ then the optimal solution is $x=0_n$. So, in pratice we only consider $\lambda <\lambda_{\max}$. 2) In $(\text{Sparse-SMART})$ the formula remains valid if there are some indices $i$ with $x_i<0$. In such cases, we should take into account the condition $Ax\geq 0$. 3) The classical SMART is
$$x^{(k+1)} = x^{(k)} \exp(A^T\log \frac{b}{Ax^{(k)}}).$$

Numerical Experiment

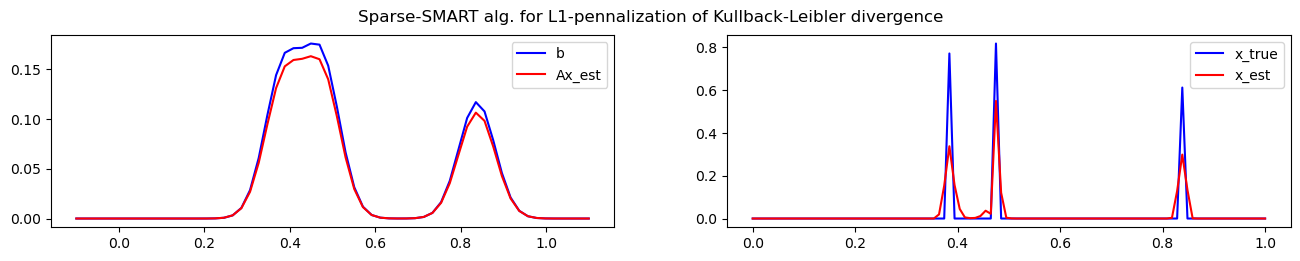
import numpy as np 
import matplotlib.pyplot as plt 

def dic(x, t, w):
  # atoms with L1-norm normalization
  diff = x.reshape(-1, 1) - t.reshape(1, -1)
  gausses = 2**(-diff**2/w**2)
  norms = np.linalg.norm(gausses, axis=0, ord=1)
  assert gausses.shape[1] == len(norms)
  return gausses/norms


def sparse_SMART(b, A, lbd, x_init, iter_stop=50):
  x = x_init 
  x_list = [x]
  for i in range(iter_stop): 
      Ax = A.dot(x)        
      r = - np.log(Ax/b)
      x = x * np.exp( (A.T).dot( r ) - lbd)
      x_list += [x]
  return x_list 


def run():
  m, n = 60, 100
  k=3
  locs = np.linspace(-0.1, 1.1, m)
  t = np.linspace(0., 1., n)
  w = 0.05
  A = dic(locs, t, w) 
  np.random.seed(1234)
  rand_indices = np.random.choice(range(n), k)
  x_true = np.zeros_like(t)
  x_true[rand_indices] = np.random.rand(k)
  b = A.dot(x_true) 

  lbd_max = np.max( (A.T).dot(b))
  lbd = 0.5*lbd_max 
  x_init = np.random.rand(n)/20.
  x_list = sparse_SMART(b, A, lbd, x_init, iter_stop=1000)
  
  fig, axs = plt.subplots(1, 2, figsize=(16, 2.5))
  ax=axs[0]
  ax.plot(locs, b, color="blue", label="b")
  ax.plot(locs, A.dot(x_list[-1]), color="red", label="Ax_est")
  ax.legend()
  
  ax=axs[1]
  ax.plot(t, x_true, color="blue", label="x_true")
  ax.plot(t, x_list[-1], color="red", label="x_est")
  ax.legend()    
  
  fig.suptitle("Sparse-SMART alg. for L1-pennalization of Kullback-Leibler divergence")
  plt.plot()
  plt.show()
  

run()

Note. In this code, it is important to notice that we should normalize the dictionary using $\ell_1$ norm instead of usual $\ell_2$ norm. Second, the initialized vector should be small, but not zero, otherwise, the whole sequence will be zeros.

References

[1]: Petra, Stefania, et al. “B-SMART: Bregman-based first-order algorithms for non-negative compressed sensing problems.” Scale Space and Variational Methods in Computer Vision: 4th International Conference, SSVM 2013, Schloss Seggau, Leibnitz, Austria, June 2-6, 2013. Proceedings 4. Springer Berlin Heidelberg, 2013.